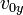Un asteroide gigantesco pasa hoy cerca a la Tierra

Científicos calculan que el meteorito de Chelyabinsk, Rusia, medía unos 15 metros de diámetro y pesaba unas 10 mil toneladas.

 |  |
 |  | |
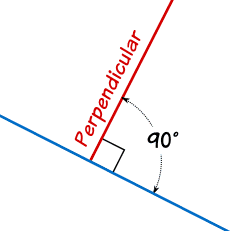
Ejemplo 1
|
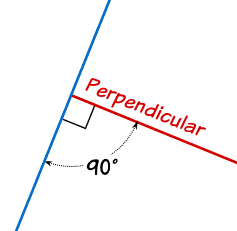
Ejemplo 2
|
 | 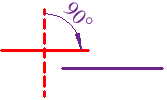 | |
Perpendiculares...
|
Girar una línea 90°
|
... ¡Paralelas!
|
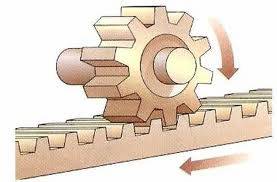 |
| El movimiento circular del piñón se transforma en movimiento lineal en la cremallera. |
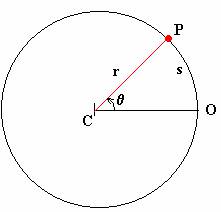 |
| Ángulo θ con centro en C. |
Resolución de ecuaciones |
| Cuando se suma o resta el mismo número en ambos miembros de una ecuación, la igualdad se mantiene. |
| Si se multiplica o divide por un mismo número a ambos lados de la igualdad, ésta se mantiene. |
Múltiplos y divisores de un número natural
| ||
Se llaman múltiplos de un número a todos los números que resultan de la multiplicación de ese número con cada uno de los naturales. Ejemplo: son múltiplos del número 2 el 4,6,8,10,12,14,16,18,20,22 y muchos más los múltiplos son infinitos como son infinitos los números naturales. | ||
Los múltiplos de un número resultan de multiplicar dicho número por cada uno de los naturales  | ||
| Existen algunas reglas que permiten decidir si un número es múltiplo de otro. Al observar la serie de los múltiplos de 2 se encuentra que todos son números pares, generalizando se puede decir que: Todo número par es múltiplo de 2. | |
Los números 3, 6, 9, 12, 15, 18, 21,.... son múltiplos de 3; observa que al sumar las cifras de los números 12, 15, 18, 21 se obtiene el número 3 o un múltiplo de 3:  | ||
| Los números 0, 10, 15, 20, 25, 30... son múltiplos de 5; todos ellos terminan en 0 y 5, por lo tanto, se dice que: Un número es múltiplo de 5 cuando su última cifra es 0 ó 5. | ||
Como todo número tiene sus múltiplos así también tienen sus divisores es decir otros números que lo dividen exactamente. | Observa los divisores de los siguientes números:
| |
 | Los divisores de un número son los que dividen a éste en forma exacta. El uno es divisor de todos los números. Todo número es divisor de sí mismo. Para determinar los divisores de un número, se buscan todos los números que lo dividen en forma exacta, es decir, el residuo debe ser cero. | |
| A continuación encontrarás algunas reglas que te harán saber cuando un número es divisible entre otro sin necesidad de estar haciendo la operación. A este conjunto de reglas le llamamos CRITERIOS DE DIVISIBILIDAD Divisibilidad por 2: un número es divisible por 2 cuando termina en cifra par. 8, 14, 54, 382, 1876 son divisibles por 2. Divisibilidad por 3: un número es divisible por 3, si la suma de los dígitos que lo componen, es múltiplo de tres. 6, 21, 69, 255, 1356 son divisibles por 3 Divisibilidad por 4: un número es divisible por cuatro si las dos últimas cifras (unidades y decenas) son dos ceros (00) o son divisibles por cuatro. Doce es divisible por cuatro por lo tanto 512 es divisible entre cuatro. Al igual que: 204 y 780, 7500... Divisibilidad por 5: un número es divisible por 5 si su último dígito es 0 o 5. Divisibilidad por 6: un número es divisible por 6, cuando es divisible por 2 y por 3 a la vez. Divisibilidad por 7: un número es divisible por 7, si el número que se obtiene al separar el último dígito, multiplicarlo por 2 y restarle el número que queda, es múltiplo de 7. Esto se ve complicado pero observa: el número 98 es divisible por 7 porque Se separa el 9 del 8, ahora se multiplica 8 x 2 = 16 y se resta 16 –9 = 7 245 es divisible por 7. porque se separa el último dígito, el 5; queda 24. Ahora se multiplica 5 x 2 = 10 y se resta 24 – 10 = 14 Divisibilidad por 9: un número es divisible por 9 si la suma de sus dígitos es múltiplo de 9. Divisibilidad por 10: un número es divisible por 10, si su último dígito es 0. Divisibilidad por 100: un número es divisible por 100, si sus dos ultimos dígitos son cero. . Divisibilidad por 1000: un número es divisible por 1000, sus tres últimos dígitos son cero. Divisibilidad por 10000: un número es divisible por 10000, sus cuatro últimos dígitos son cero. | ||
Recuerda: de la manera que leamos un texto o cualquier escrito depende que comprendamos lo que se nos quiere decir. | ||




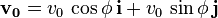

 es el módulo de la velocidad inicial.
es el módulo de la velocidad inicial. es el ángulo de la velocidad inicial sobre la horizontal.
es el ángulo de la velocidad inicial sobre la horizontal. es la aceleración de la gravedad.
es la aceleración de la gravedad.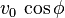 que se denomina componente horizontal de la velocidad inicial.
que se denomina componente horizontal de la velocidad inicial.

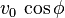 que se denomina componente horizontal de la velocidad inicial.
que se denomina componente horizontal de la velocidad inicial.

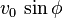 que se denomina componente vertical de la velocidad inicial.
que se denomina componente vertical de la velocidad inicial.